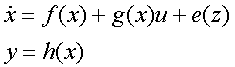
The block implements a nonlinear MIMO (multiple-input multiple-output) system with disturbance whose behaviour is defined by nonlinear state-space equations of the form
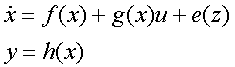
where x = (x1,x2,...,xN)T is the state vector, u = (u1,u2,...,uM)T is the input vector, y = (y1,y2,...,yP)T is the output vector and z = (z1,z2,...,zR)T is the disturbance vector of the system. Nonlinear functions f(x), g(x), h(x), e(z) can be specified either by symbolic expressions or by identifiers of symbolic variables defined in MATLAB workspace - see detailed description of block parameters below.
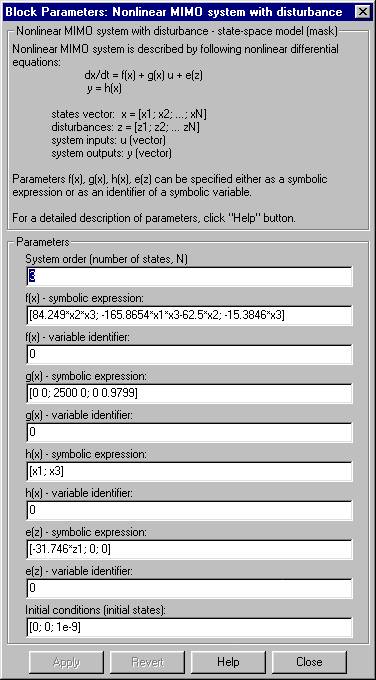
Positive integer specifying the number of state variables of the system i.e. the dimension of the system state vector x.
Symbolic expressions defining the nonlinear functions f(x), g(x), h(x), e(z) used in the state-space equations. The convention how to write these equations and mathematical operation within them is the same as the one used by Symbolic Math Toolbox. State variables have to be denoted by x1, x2, ..., xN and disturbances by z1, z2, ..., zR. If any of the f(x), g(x), h(x), e(z) functions is not specified by a symbolic expression but by an identifier of a variable (see below), it is necessary to leave corresponding field blank.
Identifiers of symbolic variables (class sym objects) containing the f(x), g(x), h(x), e(z) functions used in the state-space description of the system. If any of the f(x), g(x), h(x), e(z) functions is not specified by an identifier of a variable but by a symbolic expression (see previous parameters), it is necessary to set corresponding field to 0 (zero).
Column vector consisting of the values of the system state variables at the beginning of the simulation.