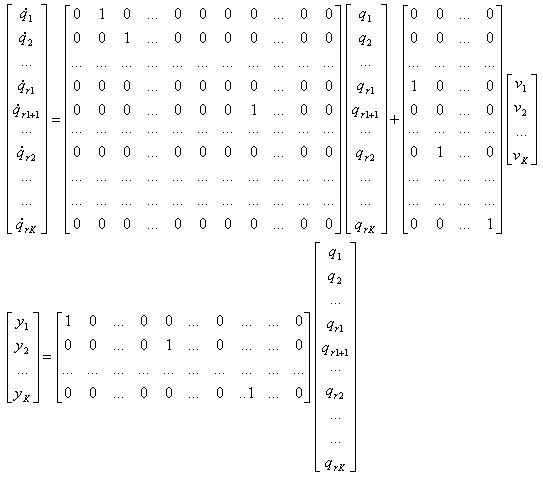
Block works as linear state-space controller designed for a MIMO system with independent SISO subsystems of rI-integrator type given by state-space description in canonical form i.e. in the form
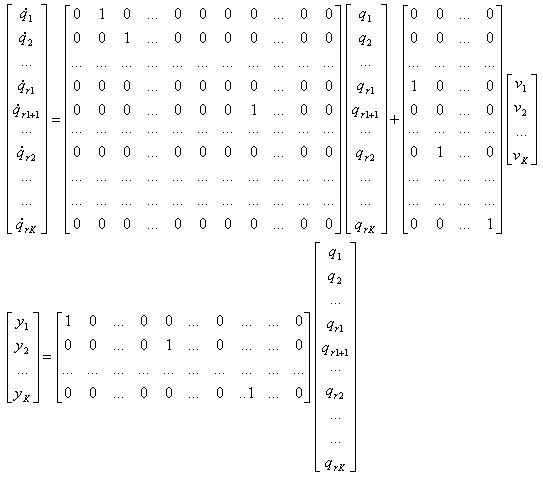
The controller is designed via pole placement during the initialization of the block, desired poles has to be specified as parameters (see below). The block is typically used in outer loop of the exact linearization scheme for SISO systems (exact linearization procedure transforms a nonlinear MIMO system to a linear system of the above type).
Important remark: This block is intended to control only linear MIMO systems of above type and does not work correctly with other systems!
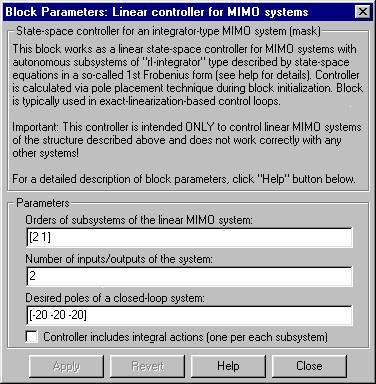
Vector of positive integer elements specifying the number of state variables belonging to different subsystems. The sum of the elements is equal to the order of the MIMO system. The number of subsystems has to be equal to the number of inputs/outputs of the MIMO system (see the following parameter).
Positive integer specifying the number of system inputs as well as the number of system outputs (if a MIMO system is composed of independent SISO subsystems the number of its inputs and outputs must be the same).
Vector of values determining the desired dynamics of the closed-loop system. The length of the vector i.e. the number of desired poles must be equal to the order of the MIMO system (in case a controller without integral actions is used) or to the order of the MIMO system increased by the number of system outputs (if controller includes integral actions). The poles are assigned to the subsystems in the order given by the elements of the vector - for example if a 3rd-order MIMO system with two subsystems, one of them 2nd-order and the other 1st-order and a controller without integral actions are considered and if desired poles are [-2 -1 -1], then the poles [-2 -1] will be assigned to the first and the pole -1 to the second subsystem. Or, if a controller with integral actions is considered, desired poles being [-2 -2 -6 -1 -3], the poles [-2 -2 -6] belong to the first and the poles [-1 -3] to the second subsystem.
Checking this box means that the state-space controller will be extended so as to include integral actions (integrals of control errors corresponding to output variables). Controller with integral actions is able to cancel the influence of disturbances to system outputs y.
See demo Exact linearization of a MIMO system