This part of the NelinSys library contains three demos illustrating the use of its function blocks for simulation of exact linearization control loops. Simulation of chosen example is started automatically, immediately after its selection from the menu (see the following picture) and during its first run it cannot be stopped - modifications of the simulation scheme are allowed only after the first simulation is over.

Simulation of exact linearization control of a 2 tanks without interaction nonlinear system. The nonlinear system is described by following equations:

Simulink simulation scheme:
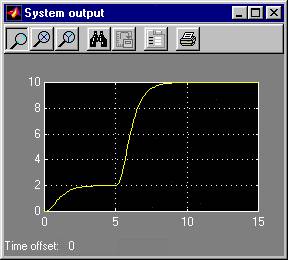
The linearizing control law as well as the transformation of state variables were calculated by the ExaktSiso application, the linear controller was designed via pole placement, desired closed-loop poles being [-2 -2]. Simulation results:

Simulation of exact linearization control of a MIMO nonlinear system DC motor with separate excitation. The system is described by following equations:
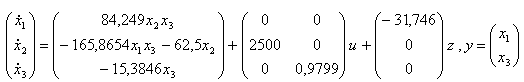
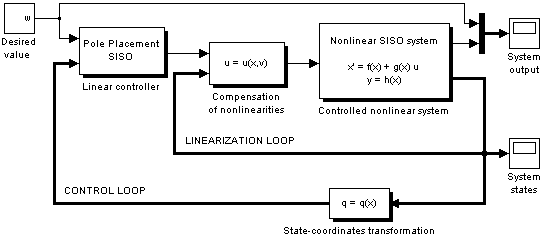
Simulink simulation scheme:

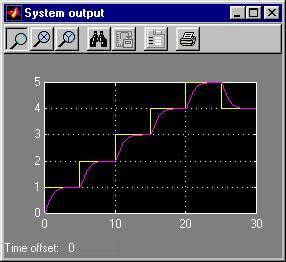
The linearizing control law as well as the transformation of state variables were calculated by the ExaktMimo application, the linear controller with integral actions was designed via pole placement, desired closed-loop poles being [-20 -20 -60 -20 -60]. The simulation shows the rise of the field current at the time instant t1 = 0s, the start of the motor without a load at the time t2 = 0.3s, its load at the time t3 = 2s and the decrease in the field current at the time t4 = 4s. Simulation results:

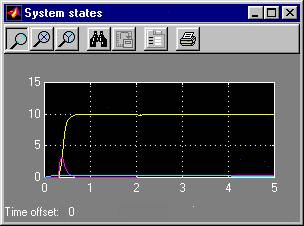
Simulation of exact linearization control of a SISO nonlinear system. The system is described by following equations:
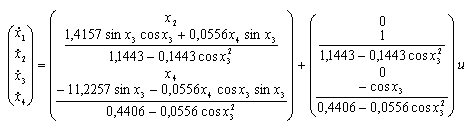
Simulink simulation scheme:

The linearizing control law as well as the transformation of state variables were calculated by the ExaktSiso application, the linear controller was designed via pole placement, desired closed-loop poles being [-2 -2]. The system contains unstable internal dynamics, which means that calculated controller is practically useless. The consequences of this instability can be seen from the state responses of the system - the x3 variable tends to infinity. Simulation results: