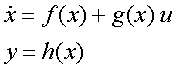
The ExaktMimo application serves as a tool for exact linearization of nonlinear MIMO systems with the same number of inputs and outputs. It calculates both the state coordinates transformation and the nonlinear feedback (linearizing control law) - two main results of the control design procedure that can be utilised in simulation or in physical implementation of the controller. There are two versions of the application - a GUI version and a text-based version.
The objective of exact linearization is to control a nonlinear system given in the form
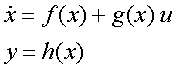
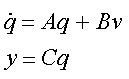
via states transformation q = q(x) and nonlinear state feedback u = u(x,v) where x = (x1,x2,...,xN)T is the states vector of the nonlinear system, u = (u1,u2,...,uP)T and y = (y1,y2,...,yP)T input and output vector of the system, respectively; vector q = (q1,q2,...,qNr)T is the states vector and v = (v1,v2,...,vP)T the input of the linear system resulting from the transformation (a more detailed discussion on exact linearization is available in literature dealing with nonlinear control systems). The ExaktMimo application automates almost every step of the exact linearization control design.

Symbolic expressions for f(x), g(x), h(x) defining the state-space description of the nonlinear system to be controlled i.e. the system to which the application should design a suitable controller via exact linearization. The convention for writing mathematical operations is the same as the one used by MATLAB's Symbolic Math Toolbox. State variables have to be denoted as x1, x2, ..., xN. Modifying of any of these fields causes deletion of previously calculated results.
Clicking this button starts the calculation of the controller i.e. the evaluation of controllability, calculation of the transformation q = q(x) and linearizing control law u = u(x,v) for a given nonlinear system. The result of these calculations will be displayed in corresponding fields (see below).
Clicking this button resets the whole form i.e. deletes all contents of the form.
Clicking this button opens the Simulink simulation Exact linearization for MIMO systems that lets the user judge the performance of the system with designed controller (see details below). Parameters of the blocks used in the simulation are taken from the ExaktMimo application via symbolic variables F, G, H (state-space description), qx (state coordinates transformation), u (linearizing control law), n (system order) and r (relative degree - vector).
Clicking this button closes all windows opened by the application and exits the program.
Clicking the Help button opens a HTML browser and displays this file in it.
This field contains conditions under which the nonlinear system is controllable - there are three options: either system is controllable (i.e. there are no further conditions to hold), or system is controllable if and only if some expression is nonzero or system is not controllable at all (in this last case, exact linearization cannot be used to design the controller). In the second case i.e. if some expression determining the controllability is involved, it is possible to print it in MATLAB Command Window in a more user-friendly fashion i.e. in a format that resembles type-set mathematics (for more information type help pretty in MATLAB Command Window).
Result - transformation equations q = q(x) for transforming state coordinates (elements of the state-space vector) of the nonlinear system to be controlled (x) into state coordinates of the linear system (q). The number of these equations is the same as system's total relative degree. By clicking the pretty button next to this field, the transformation equations can be printed in MATLAB Command Window in a more user-friendly fashion i.e. in a format that resembles type-set mathematics (for more information type help pretty in MATLAB Command Window).
Result - linearizing control law u = u(x,v) i.e. nonlinear feedback exactly compensating system nonlinearities by control action. By clicking the pretty button next to this field, the linearizing control law can be printed in MATLAB Command Window in a more user-friendly fashion i.e. in a format that resembles type-set mathematics (for more information type help pretty in MATLAB Command Window).
Evaluation of existence or nonexistence of internal dynamics in the nonlinear system. If the total relative degree (i.e. the sum of relative degrees of all subsystems) of the system is equal to the system order, there are no internal dynamics and calculated results can be used safely. However, if the total relative degree is lower than system order, it is necessary to analyze stability of system zero dynamics and only if that is stable, the exact linearization results can be used. (Remark: Mathematical analysis of zero dynamics is quite time-consuming and therefore, from practical point of view, it is often easier to analyze it by means of simulation and evaluation of time responses of system state variables).
Text-based version of the ExaktMimo application can be found in \TextRozhr subdirectory. It is run from MATLAB Command Window by typing exaktmimo. From the operational point of view, this version allows user to do everything that is possible to do with GUI version, besides, unlike the GUI version, it is able to cope with non-numeric parameters (symbols other than x) in the expressions f(x), g(x), h(x). Usage example:
Exact linearization for MIMO systems with the same number of inputs and outputs
-------------------------------------------------------------------------------
.
State-space equations: x = f(x) + g(x) u
y = h(x)
System order: 3
Specify parameters' identifiers (separated by spaces), if there are any:
System matrix: f(x) = [84.249*x2*x3; -165.8654*x1*x3-62.5*x2; -15.3846*x3]
Input matrix: g(x) = [0 0; 2500 0; 0 0.9799]
Output matrix: h(x) = [x1; x3]
Controllability: system is controllable if the following expression is nonzero:
4127779755/8 x3
Transformation equations:
q1 = x1
q2 = 84249/1000*x2*x3
q3 = x3
Relative degrees of subsystems:
2 1
Nonlinear feedback: u =
[1167173990052591 v1 x2 v2]
[----------------- x1 x3 + 1/40 x2 + 2/421245 ---- - 1/2500 -----]
[17592186044416000 x3 x3 ]
[ ]
[ 153846 10000 ]
[ ------ x3 + ----- v2 ]
[ 9799 9799 ]
Do you want to run a simulation of designed control loop? (Y/N) n
The ExaktMimo application lets user evaluate the performance of designed control loop (by means of simulation) immediately after the control law is calculated. The simulation scheme employed requires only very little user intervention before it is able to be run - parameters of the blocks Controlled system (except for initial values of state variables), State-Coordinates transformation and Compensation of nonlinearities are taken from the ExaktMimo application via symbolic variables F, G, H, u, qx, n and r.
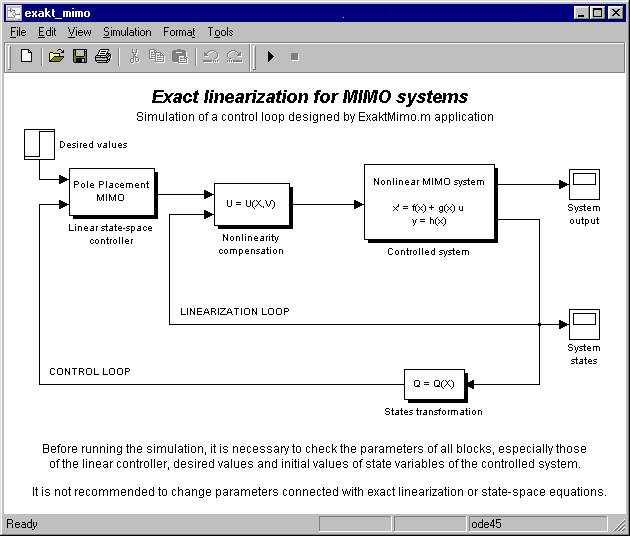
The simulation scheme contains a linear pole-placement MIMO state-space controller whose parameters are desired poles of the closed-loop system (number of these poles has to be equal to system total relative degree), however, the use of this controller is not compulsory, it can be replaced with arbitrary other suitable linear controller. Similarly, the Desired value block can be replaced with any other type of input signal.
See demo Exact linearization of a MIMO system