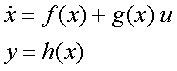
Block performs feedback compensation of system nonlinearities according to the exact linearization procedure. It is used together with the Coordinates transformation block in order to ensure a transformation of the nonlinear state-space equations of a SISO system
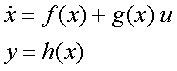
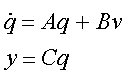
Following notations are used: x = (x1,x2,...,xN)T denotes the states vector of the nonlinear system, u and y denote the system input and output, respectively. Vector q = (q1,q2,...,qNr)T is the states vector and v the input of the linear system resulting from the transformation. The linearizing control law can be specified either by a symbolic expression or by an identifier of a symbolic variable defined in MATLAB workspace - see detailed description of block parameters below. The law can be computed by the ExaktSiso program application included in the NelinSys tool.
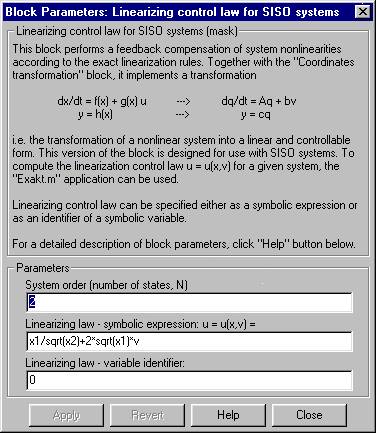
Positive integer specifying the number of state variables of the nonlinear system i.e. the length of the states vector x.
Symbolic expression defining the linearizing control law u = u(x,v); the convention for writing mathematical operations is the same as the one used by MATLAB's Symbolic Math Toolbox. State variables have to be denoted as x1, x2, ..., xN and the input of the linear system as v. If the linearizing law is not specified by a symbolic expression but by an identifier of a variable (see below), it is necessary to leave this field blank.
Identifier of a symbolic variable (a class sym object) containing the expression for u = u(x,v). If the linearizing law is not specified by an identifier of a variable but by a symbolic expression (see previous parameter), it is necessary to set this field to 0 (zero).
See demo Exact linearization of a SISO system